Image Blur

前言：

　　在討論如何做 Blur 之前，或許大家會有一個疑問是，好好的一張影像，為什麼要把它模糊化呢？模糊化之後不就變不清楚，反而不好了嗎？其實在很多情況，是需要模糊化的。

　　舉個例子來說，在做ＵＩ設計的時後，更貼切一點，在設計桌布的時候，有時候模糊化可以得到很特別的效果。

　　又或是如美圖秀秀這類ＡＰＰ，在做人臉去皺紋或去痘痘，很大部分都是做模糊化，把那塊稍微模糊，就看不到皺紋等了。

　　在研究方面，模糊化可能是很多取 Feature 之前的前置動作，因為影像可能包含一些雜訊，這些雜訊可能值突然的高或突然的低，如果靠模糊化，可以把這些值抹掉，做出來的結果就比較不會被這些雜訊所影響。

　　目前主要做模糊化有兩個面向，一個是在 Spatial Domain (值域)，另外一個則是在 Frequency Domain（頻域），值域部分，透過簡單的數學跟陣列操作就能完成，而在頻域則是透過濾掉高頻來達到模糊化的效果。以下會一一講解。

值域：

　　在值域這裡要做模糊化很簡單，基本觀念就是讓每一個 pixel，都會被周圍的 pixels 影響，把整體平均掉，看起來就會比較平滑模糊了。

　　以１-Ｄ的例子來說，我們讓每一個值都跟周圍三個平均來當作結果，整體看起來就不會差距這麼懸殊了，如下例子：

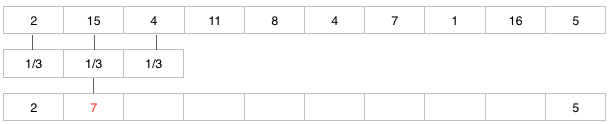
　　其中７＝１／３＊（２＋１５＋４）

　　用同樣的方式，我們可以把整個陣列都算出來，結果如下：

　　整體而言，起伏變小了，我們可以把兩張圖弄出來給大家看看，如下：

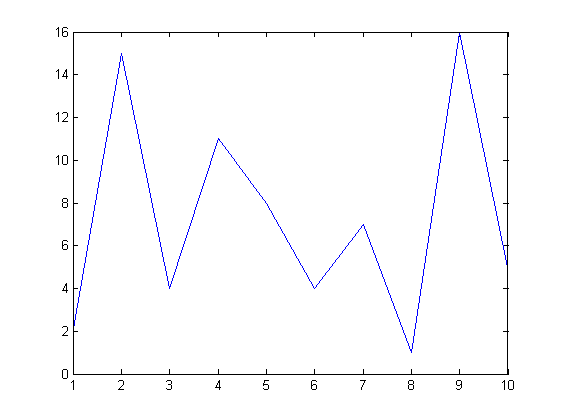
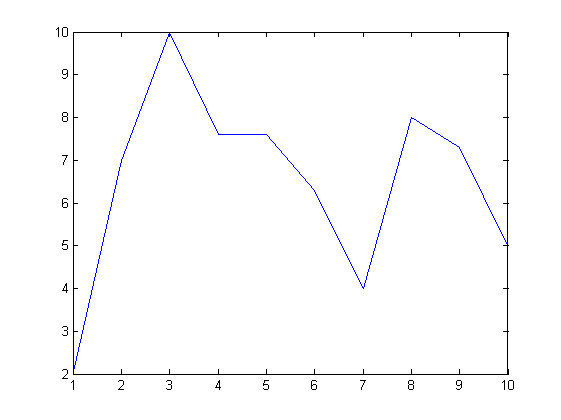
　　上圖為原先陣列畫出來的圖，而下圖則是結果，明顯看起來平滑多了，比較不會快速起伏，當然想要更加 blur 可能可以使用不同的權重，如考慮周圍五個，然後每一個佔的比例是１／５，或是有時候不想要那麼模糊，可能可以１／６, ２／３, １／６，端看使用的情況是怎樣。

　　這些權重，普遍會稱作 kernel 或 filter，有時候也會叫做 blur kernel 等。

　　此外，注意到上面的例子裡，兩端沒有辦法計算，這在使用大一點的 kernel 時尤為明顯，解決方法有很多，比方說在旁邊補上一些０讓他可以運算，或是補上對稱的值等。

　　講完１-Ｄ之後，回過頭來講影像處理，在影像中作法其實相當類似，只是 blur kernel 是２-Ｄ的，如下面這個例子：

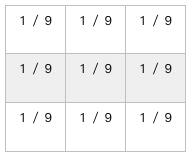
　　為了效果明顯，以下展示使用５＊５kernel 做出來的結果：

　　並附上 matlab source code。

tree = imread('tree.jpg');

kernel = 1/25*ones(5,5);

result = zeros(size(tree));

for k = 1:size(tree,3)
    for i = 4:size(tree,1)-3
        for j = 4:size(tree,2)-3
            for bx = -3:1
                for by = -3:1
                    result(i,j,k) = result(i,j,k)+ ...
                        kernel(bx+4,by+4)*tree(i+bx,j+by,k);
                end
            end
        end
    end
end

result = uint8(result);
imshow(result);

　　其實這個 kernel 的概念可以繼續延伸，可以做到如簡單的 edge detection 運用類似二次微分通過零點的概念來實現，以下是使用 laplacian kernel 做出來的結果，可以看到可以稍微看出邊緣，如果圖不要太複雜，用此方法就能很完美的找到邊在哪。

頻域：

　　頻域的想法主要是在 frequency domain 中低頻代表的是圖片整體的樣子，而高頻則是如邊之類的細節。可以思考看看，整體的樣子通常不會有劇烈變化，所以就是低頻，而物體跟物體之間會有邊，在邊的地方頻率會有劇烈變化，所以是高頻。換言之，如果要在頻域完成 blur 那麼我們就需要濾掉高頻訊號。

　　講到濾波器，在訊號處理中有相當多種濾波器，或稱作 window，如三角形，正方形，高斯濾波等，做出來的結果也會有所差異。

　　以下展示正方形濾波跟高斯濾波的差別，正方形因為頻譜轉換之後會是 sinc function 所以會有波浪的樣子，而高斯濾波頻域跟值域都是一樣，所以效果相對好。

　　第一張為原圖，之後依序是正方形及高斯。

　　最後附上 matlab source code，在 code 中還有實現 Butterworth 的濾波器，不過結果跟高斯相當類似就沒有放結果了。

close all;

tree = imread('tree.jpg');

tree = rgb2gray(tree);
figure('NumberTitle', 'off', 'Name', 'input');
imshow(tree, []);

TREE = fftshift((fft2(tree)));

%ideal low pass filter
H = zeros(800,802);
for i=1:512
    for j = 1:512
        if sqrt((i-400)^2 + (j-401)^2) < 20
             H(i,j) = 1;
        end
    end
end
B = TREE.*H;
tree = (ifft2(ifftshift(B)));
figure('NumberTitle', 'off', 'Name', 'ideal low');
imshow(tree, []);

%gaussian low pass filter
sigma = 20;
[x, y]=meshgrid(-401:400,-400:399);
f=exp(-x.^2/(2*sigma^2)-y.^2/(2*sigma^2));
B = TREE.*f;
tree = (ifft2(ifftshift(B)));
figure('NumberTitle', 'off', 'Name', 'gaussian low');
imshow(tree, []);

%Butterworth low pass filter
n = 2;
sigma = 20;
[x, y]=meshgrid(-401:400,-400:399);
f=1./(1+((sqrt(x.^2+y.^2))./20).^(2*n));
B = TREE.*f;
tree = (ifft2(ifftshift(B)));
figure('NumberTitle', 'off', 'Name', 'butterworth low');
imshow(tree, []);

結語：

　　blur 是影像處理的基本功，很多地方都會用到，這篇只是介紹最基礎的部分，如上面所述，其實 kernel 有很多更厲害的用途，當然在頻域這邊也是。而頻域跟值域只是一體兩面，能夠從不同角度看待這件事情，下次有時間或許會補完其他方面的應用，如上述的 laplacian kernel 等。

　　最後，如有錯誤歡迎告知，感謝。：Ｄ

前言：

值域：

頻域：

結語：

相關文章：